Imagine a world where complex electrical circuits, those intricate webs of wires and components, could be easily understood and manipulated. Sounds like a dream, right? But what if I told you that the magic key to unlock this world is hidden within a powerful mathematical tool – Boolean algebra?
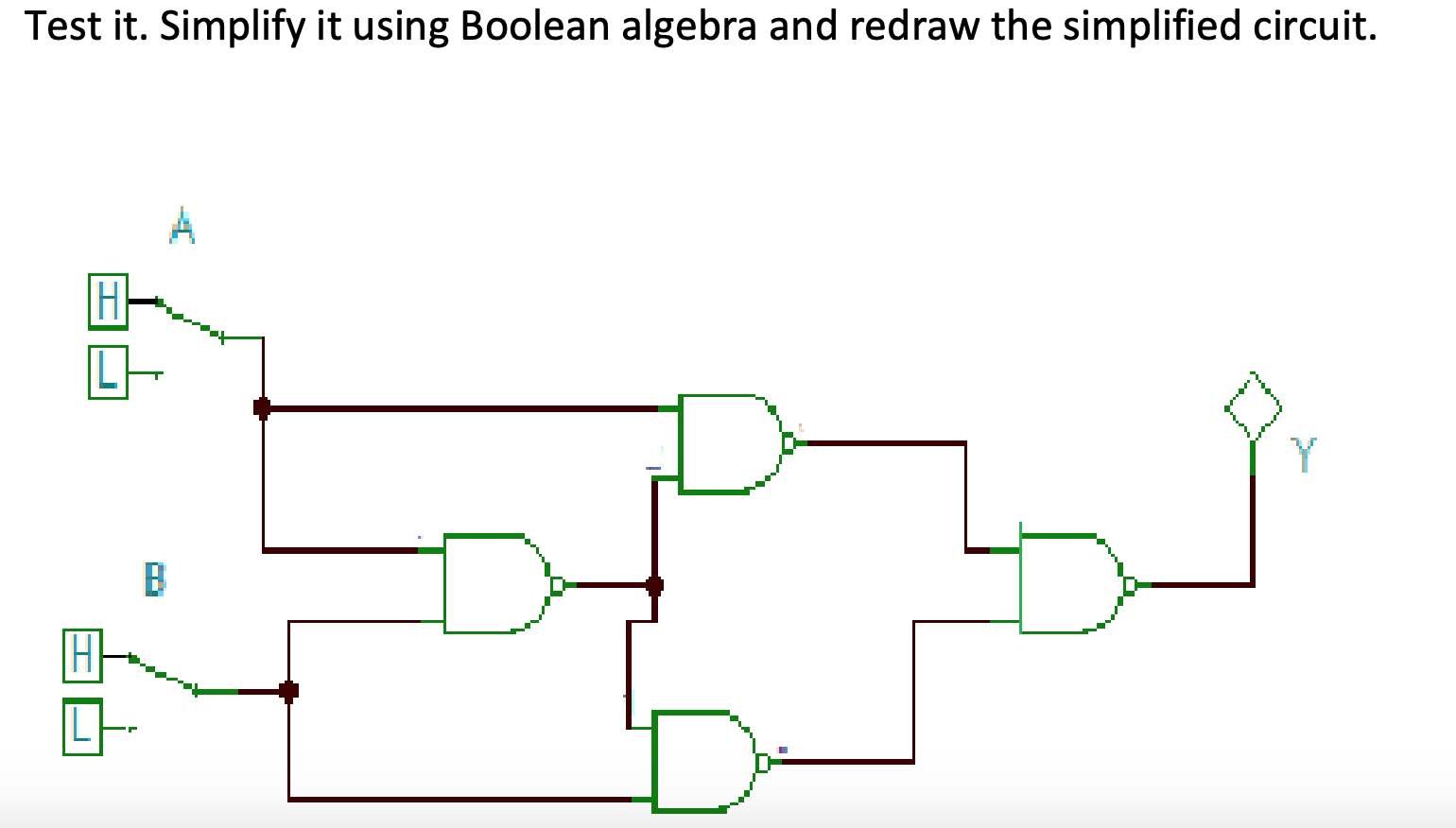
Image: www.chegg.com
This intriguing branch of mathematics, named after the brilliant English mathematician George Boole, lays the foundation for simplifying complex digital circuits, reducing their size, cost, and power consumption, while boosting their performance. In this journey, we’ll delve into the captivating realm of activity 2.1.4 – circuit simplification using Boolean algebra. You’ll uncover its wonders, master essential concepts, and learn to effortlessly navigate the intricate landscapes of digital circuits.
The Building Blocks of Digital Logic
Boolean algebra is the bedrock of digital electronics. It’s a language built upon logic gates, each representing a fundamental operation that manipulates binary values, 0 and 1. These gates, such as AND, OR, NOT, XOR, and others, act like tiny decision-makers, controlling the flow of signals in a circuit. By combining these gates, we can create complex circuits capable of performing a vast range of operations.
Think of it like this: Imagine you’re building a complex machine. Each logic gate is like a simple gear, performing a specific task. By combining different gears in the right way, you can build a powerful machine that can perform elaborate functions. Boolean algebra gives us the tools to design these gears and understand how they work together, paving the way for the creation of sophisticated digital systems.
Activity 2.1.4: Unveiling the Secrets of Circuit Simplification
Activity 2.1.4 is your first encounter with the transformative power of Boolean algebra in the context of digital circuits. It introduces you to the fundamental concepts of simplifying circuits using Boolean algebra, empowering you to unravel complex circuits and understand their behavior.
Imagine you’re presented with a complex circuit diagram – a tangled web of gates and connections. It’s daunting, a maze of logic. But, armed with Boolean algebra, you unlock the ability to translate this intricate web into simple, elegant mathematical expressions. You then leverage the powerful rules of Boolean algebra, like the distributive law, De Morgan’s theorem, and the consensus theorem, to manipulate these expressions, eliminating redundancies and simplifying the circuit. It’s a bit like turning a jumbled puzzle into a beautifully organized arrangement, revealing the core logic beneath the complexity.
Navigating the Labyrinth of Boolean Algebra
But how do we navigate this labyrinth of Boolean algebra? The key lies in mastering its rules and applying them to the circuit’s logic expressions. Through practice and understanding, you’ll be able to effortlessly read these expressions, recognizing patterns and applying the appropriate simplification techniques.
For example, consider the Boolean expression A + (A * B). You quickly recognize that it can be simplified to simply A using the distributive law. It’s like revealing a hidden shortcut in the circuit’s logic, streamlining its operation and making it more efficient.
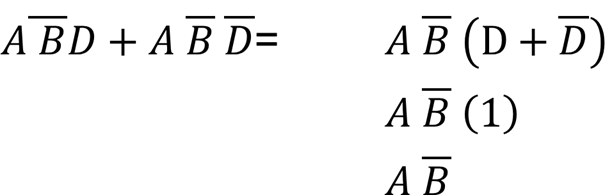
Image: grace.bluegrass.kctcs.edu
The Benefits of Circuit Simplification
The benefits of simplifying circuits are remarkable. By reducing the number of logic gates, you can achieve several advantages:
- Reduced Cost: Simplified circuits require fewer components, leading to lower manufacturing costs.
- Improved Performance: Simplifying circuits reduces the number of delays introduced by logic gates, leading to faster and more efficient operation.
- Reduced Power Consumption: Fewer gates mean less power consumption – a big win in the world of electronics where energy efficiency is essential.
- Enhanced Reliability: A simpler circuit is less prone to errors, leading to improved reliability and stability.
Unleashing the Power of Karnaugh Maps
Karnaugh maps are your secret weapon in the world of Boolean algebra. These visual tools provide a structured way to simplify Boolean expressions. They help you identify and group together adjacent terms in the expression, revealing opportunities to minimize the circuit complexity.
Imagine plotting a logic expression on a Karnaugh map, like a landscape with peaks and valleys. By grouping together adjacent peaks, you effectively identify areas where the logic can be simplified. It’s like finding a hidden valley that connects two mountains, allowing you to navigate the landscape with greater efficiency.
Real-World Applications: The Impact of Boolean Algebra
The impact of Boolean algebra extends far beyond the realm of activity 2.1.4. It serves as the backbone for a wide range of modern technologies:
- Computer Architecture: Boolean algebra is the driving force behind the design of processors and computer memory, shaping the very foundation of our digital world.
- Digital Design: Circuit simplification using Boolean algebra is vital in designing everything from mobile phones to complex control systems. It allows engineers to create efficient, reliable, and cost-effective digital devices.
- Artificial Intelligence: Boolean algebra plays a significant role in the development of artificial intelligence (AI), enabling the creation of logical reasoning systems and decision-making algorithms.
- Computer Science: Boolean algebra is fundamental to various computer science fields, including database systems, network security, and cryptography, empowering these domains with robust logic and problem-solving capabilities.
Expert Insights: Tips for Mastering Boolean Algebra
To truly unlock the power of Boolean algebra, experts in the field offer these invaluable insights:
- Focus on the Basics: Understand the fundamental concepts of logic gates and Boolean operations thoroughly before venturing into complex circuit simplification.
- Practice Makes Perfect: Practice solving various circuit simplification exercises using Karnaugh maps and Boolean algebra rules.
- Visualize the Logic: Use visual tools like Karnaugh maps or truth tables to aid in understanding the logic of circuits.
- Don’t Be Afraid to Ask for Help: Seek guidance from teachers, classmates, or online resources if you encounter difficulties.
Activity 2.1.4 Circuit Simplification Boolean Algebra
https://youtube.com/watch?v=RLkA6zsyrew
Beyond Activity 2.1.4: Your Journey into the World of Digital Logic
Activity 2.1.4 is just the beginning of a fascinating journey into the world of Boolean algebra and digital logic design. As you delve deeper, you’ll discover a universe of possibilities – from designing advanced microchips to creating intelligent systems that challenge the boundaries of human ingenuity.
So, embrace the power of Boolean algebra, unravel the mysteries of digital circuits, and become a master of the logic that defines our digital world. The possibilities are truly limitless!






