Have you ever wondered how a seemingly motionless object, like a book resting on a table, is actually being subjected to a complex interplay of forces? Or how a plane can soar through the air, defying gravity? These are just a few examples of the fascinating world of forces, a fundamental concept in physics that governs the motion of everything around us. Understanding forces is not just about passing physics tests; it’s about unraveling the invisible threads that connect all objects in the universe. This exploration delves into the intricate world of force tables and vector addition, equipping you with the knowledge to confidently navigate your pre-lab assignments and beyond.

Image: www.chegg.com
The study of forces often begins with the concept of vector addition, a powerful tool for understanding how multiple forces act upon an object. To visualize and quantify these forces, physics labs often utilize a force table, a crucial instrument that allows us to experimentally explore the principles of vector addition and equilibrium. This pre-lab guide aims to equip you with a thorough understanding of the fundamental concepts, essential definitions, and practical tips for confidently tackling your pre-lab exercises and experiments.
Understanding the Force Table: A Gateway to Vector Addition
The force table is a circular platform with a central ring and multiple pulleys situated around the circumference. Strings attached to weights hang over these pulleys and are connected to the central ring. Each string represents a force vector, characterized by its magnitude (the weight) and direction (determined by the angle of the string). The central ring serves as the point of application for all the forces, allowing us to study their combined effect.
At the heart of understanding force tables lies the concept of vector addition. Vectors, unlike scalars, possess both magnitude and direction. Force is a vector quantity, and when multiple forces act on an object, their combined effect is determined by the vector sum of these individual forces.
Key Concepts in Vector Addition
Before delving into the mechanics of the force table, it’s crucial to grasp the fundamental principles of vector addition. Here are some key concepts to keep in mind:
- Graphical Representation: Vectors are visually represented by arrows, where the arrow’s length signifies the magnitude and its direction indicates the force’s direction.
- Head-to-Tail Method: To find the resultant vector, which is the vector sum of multiple forces, we use the head-to-tail method. We place the tail of the second vector at the head of the first vector, and then draw a line from the tail of the first vector to the head of the second vector. This new vector represents the sum of the two forces.
- Parallelogram Method: An alternative method for finding the resultant vector is the parallelogram method. We place the tails of the two vectors at the same point, then complete a parallelogram, drawing lines parallel to each vector. The diagonal of the parallelogram starting from the common tail represents the resultant vector.
- Equilibrium: When the vector sum of all forces acting on an object is zero, the object is said to be in equilibrium. This means the object is either at rest or moving at a constant velocity.
Navigating the Force Table: A Practical Guide
Now that we’ve established the underlying principles of vector addition, let’s dive into the specifics of using the force table to validate these concepts.
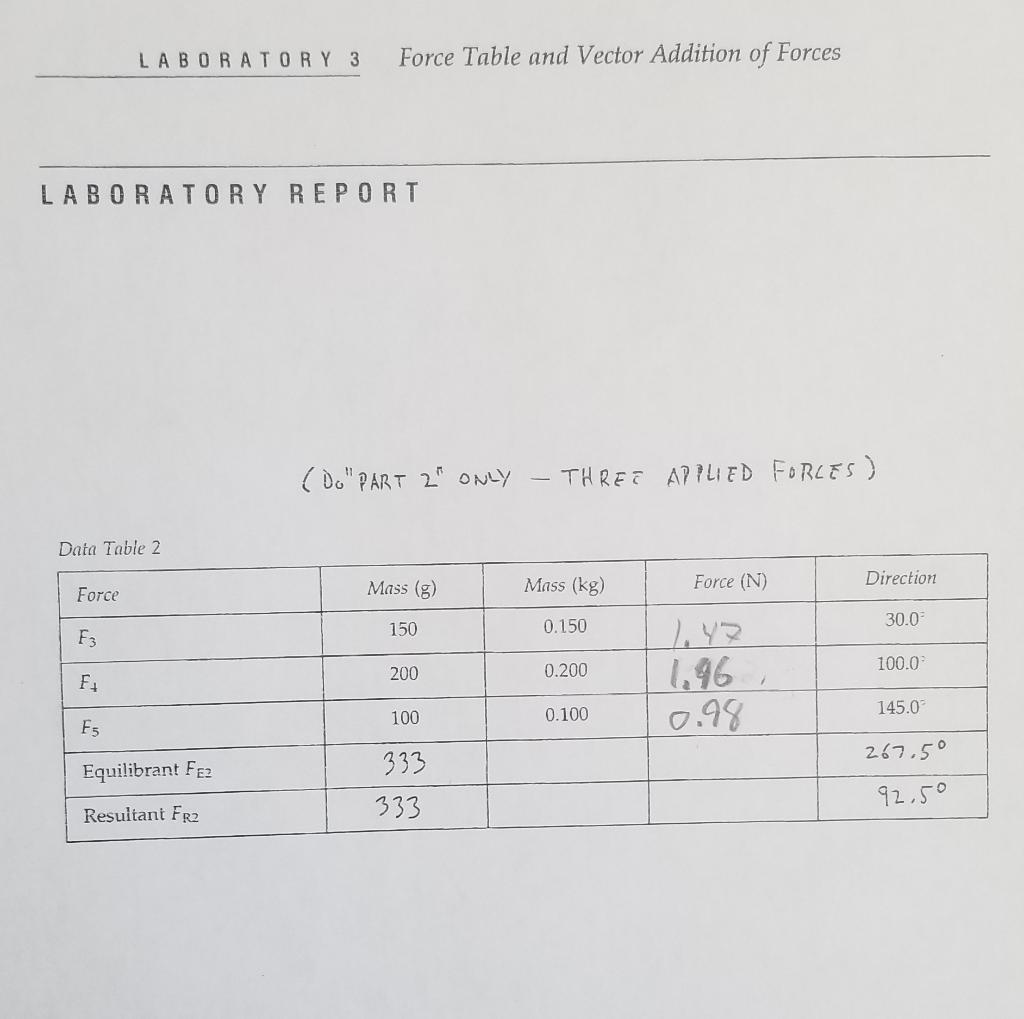
Image: www.chegg.com
Pre-Lab Exercises: Preparing for the Experiment
- Determine the Forces: The pre-lab usually involves calculating the magnitudes and directions of forces that would result in equilibrium when applied to the central ring.
- Vector Addition Calculations: Use the head-to-tail or parallelogram method to find the resultant vector (the vector sum) of the given forces.
- Force Table Configuration: Based on your calculations, determine the angles at which each force should be applied to achieve equilibrium. This often involves balancing the forces in opposing directions.
Performing the Experiment
- Setting up the Force Table: Position the pulleys at the angles calculated in your pre-lab.
- Applying the Forces: Attach weights to each string, ensuring the weights correspond to the magnitudes of the forces you determined.
- Adjusting for Equilibrium: Carefully adjust the angles and/or weights until the central ring is stationary, indicating that the forces are in equilibrium.
Understanding the Results: Interpreting the Data
Once you’ve successfully achieved equilibrium on the force table, it’s time to analyze your results and ensure they align with the theoretical calculations. This often involves the following steps:
- Measuring the Angles: Record the precise angles at which each force is applied.
- Calculating the Resultant Vector: Using the measured angles and magnitudes of each force, calculate the resultant vector.
- Comparing Results: Compare your calculated resultant vector to the actual observed equilibrium condition. If they align closely, it validates the principles of vector addition and the accuracy of your experimental setup.
Understanding the Significance: Real-World Applications of Vector Addition and Force Tables
The application of force tables and vector addition extends far beyond the confines of a physics lab. These concepts are essential for understanding a wide range of real-world phenomena, including:
- Engineering: Engineers utilize vector addition principles to analyze forces acting on structures like bridges, buildings, and airplanes. This is crucial for ensuring structural integrity and safety.
- Fluid Mechanics: Understanding the forces acting on objects submerged in fluids, such as boats and submarines, relies heavily on vector addition principles.
- Medical Applications: Medical professionals use vector addition to analyze the forces acting on bones and joints, aiding in diagnosis and treatment of musculoskeletal disorders.
- Robotics: Vector addition is fundamental in developing and controlling robots, enabling them to navigate complex environments and perform various tasks.
Beyond the Lab: Further Applications and Exploration
The concepts of vector addition and force tables provide a foundation for understanding not just the physical world but also the interactions between objects. As you progress in your physics studies, you’ll encounter more complex scenarios where these principles play an essential role. To further deepen your understanding, consider exploring these topics:
- Projectile Motion: Applying vector addition to analyze the horizontal and vertical components of a projectile’s motion, allowing you to understand its trajectory.
- Torque and Rotational Motion: Vector addition principles are extended to analyze torques, which are rotational forces acting on an object.
- Work and Energy: The concepts of force and displacement, both vector quantities, form the foundation of understanding work and energy.
Force Table And Vector Addition Of Forces Pre Lab Answers
Conclusion: Embracing the Power of Vector Addition
As you embark on your journey of understanding the world through the lens of physics, remember that the seemingly simple concept of vector addition is a powerful tool that unlocks the intricacies of how forces act upon objects. The force table, with its intuitive design, provides a platform to visualize and quantify these concepts, equipping you with the knowledge to confidently navigate your pre-labs and explore the complexities of the physical world. By understanding the foundation of vector addition, you gain a deeper appreciation for the forces that govern our universe, from the motion of celestial bodies to the intricate workings of the human body. Let this journey inspire you to further explore the fascinating world of physics and its remarkable applications in all aspects of our lives.






